Cho tứ giác abcd nội tiếp đường tròn

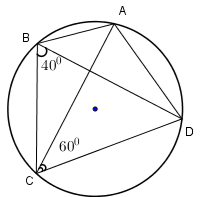
Cho tứ giác (ABCD) nội tiếp đường tròn (left( O ight)) (hình (1) ). Chọn xác minh đúng nhất? 

Bạn đang xem: Cho tứ giác abcd nội tiếp đường tròn

Vì tứ giác (ABCD) là tứ giác nội tiếp nên

(widehat BDC = widehat BAC) (hai góc nội tiếp cùng chắn cung (BC) )

(widehat ABC + widehat ADC = 180^circ ) (tổng hai góc đối bằng (180^circ ) )

(widehat DCB = widehat BAx) (góc ko kể tại một đỉnh bởi góc trong trên đỉnh đối với đỉnh đó)

Phương án A, B, C đúng

Cho tứ giác (ABCD) nội tiếp đường tròn (left( O ight)) (hình (1) ). Chọn xác định đúng nhất?

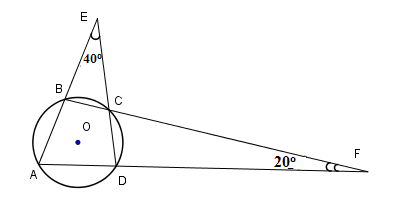
Cho nửa đường tròn (left( O;R ight)) đường kính (BC.) lấy điểm (A) bên trên tia đối của tia (CB.) Kẻ tiếp tuyến đường $AF,Bx$ của nửa đường tròn (left( O ight)) (với (F) là tiếp điểm). Tia (AF) giảm tia (Bx) của nửa đường tròn trên (D.) khi đó tứ giác (OBDF) là:

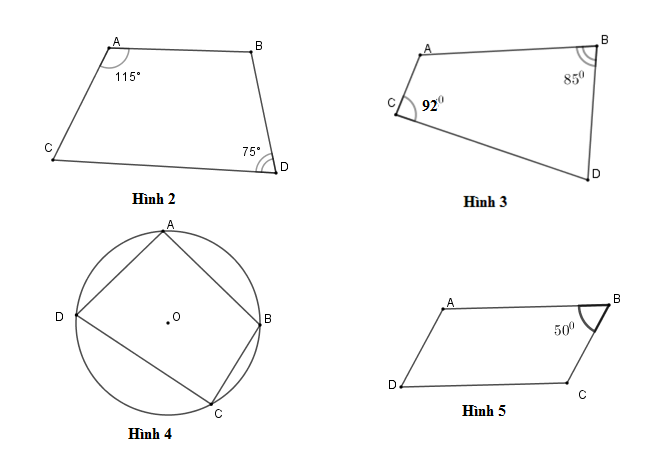
Tứ giác $ABCD$ nội tiếp mặt đường tròn gồm hai cạnh đối $AB$ và $CD$ giảm nhau tại $M$ cùng $widehat BAD = 70^0$ thì $widehat BCM = ?$

Cho con đường tròn $left( O ight)$ 2 lần bán kính $AB$ . Hotline $H$ là vấn đề nằm thân $O$ với $B$. Kẻ dây $CD$ vuông góc cùng với $AB$ trên $H$ . Trên cung nhỏ tuổi $AC$ mang điểm $E$ kẻ $CK$ vuông góc $AE$ tại $K$ . Đường thẳng $DE$ cắt $CK$ trên $F$. Lựa chọn câu đúng:

Cho (Delta ABC) cân tại (A) có (widehat BAC = 120^0.) trên nửa mặt phẳng bờ (BC) không cất đỉnh (A), lấy (D) sao cho (BCD) là tam giác đều. Khi đó

Cho tam giác $ABC$ nhọn nội tiếp con đường tròn$left( O ight)$ . $M$ là điểm thuộc cung nhỏ tuổi $AC$ (cung (CM

Xem thêm: