Công thức hàm số mũ và logarit
Hàm số mũ với logarit - phần kỹ năng và kiến thức rộng cùng rất quan trọng đặc biệt đối với học viên THPT. Vì chưng thế, để làm chủ hàm mũ logarit không phải là điều thuận tiện nếu không có phương pháp và trong suốt lộ trình ôn tập ráng thể. Trong nội dung bài viết này, capnuochaiphong.com để giúp các em nạm chắc định hướng và giải gọn gàng mọi bài tập về chuyên đề hàm số mũ cùng logarit.
Trước khi đi vào rõ ràng các phần hàm mũ và hàm logarit, những em đọc bảng sau đây để thay được những đánh giá và nhận định chung của các thầy cô trình độ chuyên môn capnuochaiphong.com về phần kiến thức và kỹ năng hàm số mũ cùng logaritnày:

Chi tiết rộng về hàm số mũ với hàm số logarit, capnuochaiphong.com gửi khuyến mãi ngay các em học viên file tổng hợp không thiếu và cụ thể lý thuyết siêng đề hàm số mũ cùng logarit trong chương trình THPT. Những em nhớ cài đặt về nhằm tiện trong việc ôn tập toán 12 hàm số mũ và logarit nhé!
Tải xuống file không thiếu thốn lý thuyết về hàm số mũ với logarit
1. Ôn tập định hướng về hàm số mũ và logarit
Định nghĩa là nền tảng gốc rễ để giải đầy đủ vấn đề, đặc thù và định lý nâng cấp sau này của hàm số mũ và logarit. Vày vậy trước lúc ôn tập triết lý về hàm mũ với hàm logarit, bọn họ cần đọc về từng định nghĩa căn bản của từng dạng hàm số.
Bạn đang xem: Công thức hàm số mũ và logarit
1.1. Tổng hợp triết lý hàm số mũ
1.1.1 Định nghĩa của hàm số mũTheo kỹ năng và kiến thức THPT đã có được học, Hàm số $y=f(x)=a^x$ cùng với a là số thực dương không giống 1 được call là hàm số nón với cơ số $a$.
Một số ví dụ về hàm số mũ: $y=2^x^2-x-6$, $y=10^x$,...
1.1.2. Đạo hàm với tính chấtTa có công thức đạo hàm của hàm số nón như sau:

Lưu ý: Hàm số mũ luôn luôn có hàm ngược là hàm logarit
Chúng ta cùng xét hàm số mũ dạng tổng thể $y=a^x$ cùng với $a>0$, $a eq 1$ có tính chất sau:

Đồ thị của hàm số nón được điều tra khảo sát và vẽ dạng bao quát như sau:
Xét hàm số nón $y=a^x$ (a > 0; a ≠ 1).
• Tập xác định: $D=mathbbR$.
• Tập giá bán trị: T = (0; +∞).
• khi $a>1$ hàm số đồng biến, khi $0
Khảo gần cạnh đồ thị:
+ Đi qua điểm $(0;1)$
+ Nằm phía bên trên trục hoành.
+Nhận trục hoành có tác dụng tiệm cận ngang.
• ngoài mặt đồ thị:
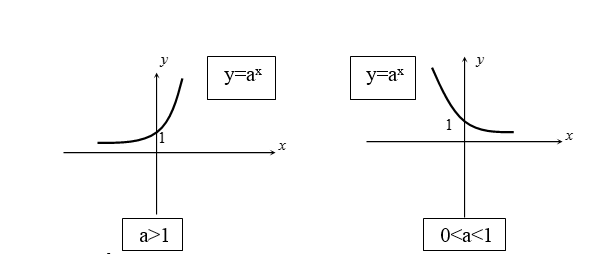
Chú ý: Đối với những hàm số nón như $y=(frac12)^x$, $y=10^x$, $y=e^x$, $y=2^x$ đồ vật thị của hàm số mũ sẽ có được dạng đặc biệt quan trọng như sau:
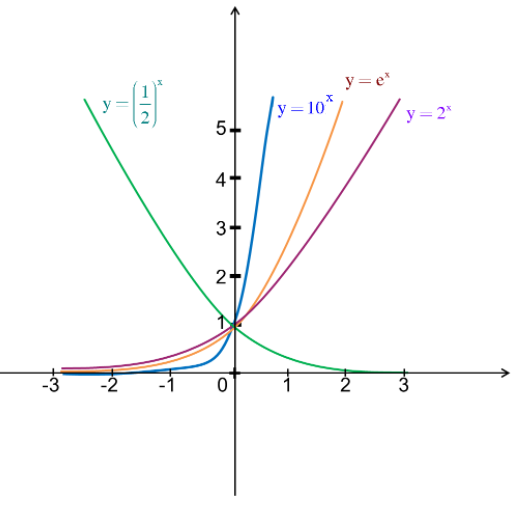
1.2. Tổng hợp định hướng về hàm số logarit
1.2.1. Định nghĩaVì đều phải có “xuất thân” từ bỏ hàm số, cho nên hàm mũ và hàm logarit bao hàm nét tương đồng nhau trong định nghĩa. Hàm logarit diễn đạt theo ý riêng hiểu đơn giản dễ dàng là hàm số có thể biểu diễn được bên dưới dạng logarit. Theo công tác Đại số THPT những em đã có được học, hàm logarit có định nghĩa bởi công thức như sau:
Cho số thực $a>0$, $a eq 1$,$x>0$, hàm số $y=log_ax$ được điện thoại tư vấn là hàm số logarit cơ số $a$.
1.2.2. Đạo hàm và tính chấtCho hàm số $y=log_ax$. Lúc ấy đạo hàm hàm logarit bên trên là:
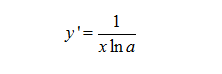
Trường hợp tổng quát hơn, cho hàm số $y=log_au(x)$. Đạo hàm hàm số logarit là:
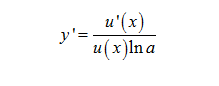
Xét hàm số logarit $y=log_ax$(a > 0; a ≠ 1), ta điều tra khảo sát và vẽ đồ dùng thị hàm số theo công việc sau:
Tập xác định: D = (0; +∞).Tập giá chỉ trị:
+ Đi qua điểm (1; 0).
+ nằm ở vị trí bên yêu cầu trục tung.
+ nhận trục tung có tác dụng tiệm cận đứng.
Hình dạng vật thị: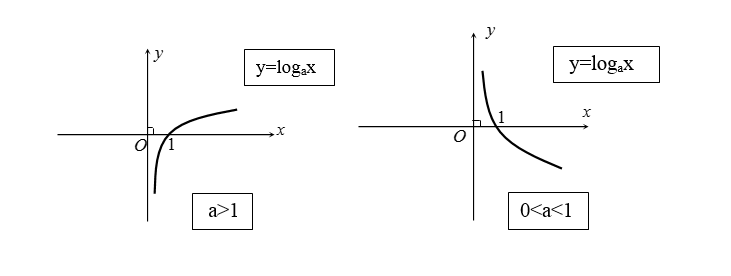
2. Các dạng bài xích tập hàm số mũ và logarit
Đây là phần đặc biệt nhất của nội dung bài viết về hàm mũ cùng hàm logarit. capnuochaiphong.com đang tổng hợp cho những em toàn bộ các dạng bài tập cơ bản và thường gặp gỡ nhất của hàm mũ cùng hàm logarit. Ở mỗi dạng sẽ sở hữu ví dụ minh hoạ kèm giải cụ thể để những em tham khảo.
2.1. Tổng hợp các dạng bài bác tập hàm số mũ
Dạng 1: tra cứu hàm số có đồ thị mang lại trước cùng ngược lại
Đây là dạng cơ bạn dạng và siêu dễ lộ diện trong những câu trắc nghiệm đề thi đại học hoặc trong lịch trình toán 12 hàm số mũ và logarit. Để có tác dụng được những bài tập hàm số mũ tất cả đồ thị mang lại trước, ta triển khai theo 2 cách sau:
Bước 1: Quan sát dáng thứ thị, tính đối chọi điệu,…của những đồ thị bài cho.
Xem thêm: Song Ji Hyo'S Brother Cheon Seong Moon To Debut As An Actor
Bước 2: Đối chiếu cùng với hàm số bài xích cho và chọn kết luận
Chúng ta cùng xét ví dụ minh hoạ dưới đây để làm rõ hơn về dạng bài bác tập hàm số nón này:
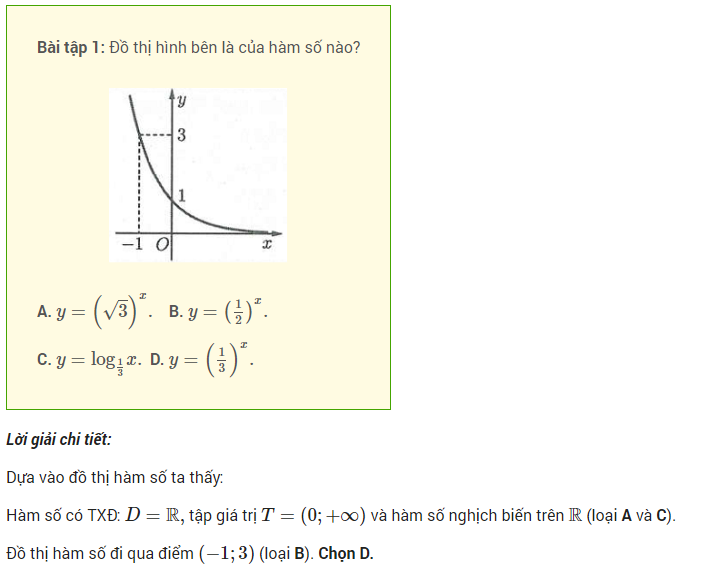
Dạng 2: Tìm quan hệ giữa các cơ số lúc biết đồ thị
Bước 1: quan tiền sát những đồ thị, nhận xét về tính chất đơn điệu để dấn xét những cơ số.
+ Hàm số đồng thay đổi thì cơ số lớn hơn 1
+ Hàm số nghịch trở nên thì cơ số to hơn 0 và nhỏ dại hơn 1
Bước 2: So sánh các cơ số phụ thuộc phần vật thị của hàm số.
Bước 3: phối kết hợp các đk ở trên ta được quan hệ cần tìm.
Đối với một trong những bài toán phức tạp hơn thế thì ta cần chú ý thêm đến một trong những yếu tố khác ví như điểm đi qua, tính đối xứng,…


Dạng 3: Tính đạo hàm những hàm số mũ
Đối với dạng bài xích tính đạo hàm của những hàm số nón trong chăm đề toán 12 hàm số mũ và logarit, ta yêu cầu nắm vững những công thức đạo hàm của tổng hiệu tích thương để áp dụng giải bài bác toán. Chũm thể, các em tiến hành theo công việc sau:
Bước 1: Áp dụng những công thức tính đạo hàm của tổng, hiệu, tích, thương nhằm tính đạo hàm hàm số vẫn cho.
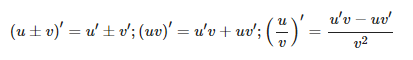
Bước 2: Tính đạo hàm những hàm số thành phần nhờ vào công thức tính đạo hàm những hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
Bước 3: đo lường và kết luận.
Ta thuộc xét ví dụ minh hoạ sau:

Dạng 4: Tính giới hạn hàm số mũ
Ở dạng này, những em áp dụng những công thức tính giới hạn đặc biệt để tính toán:
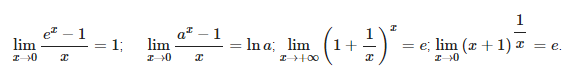
Cách làm ví dụ được minh hoạ làm việc ví dụ sau:
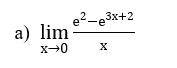
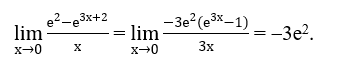
Dạng 5: kiếm tìm GTLN, GTNN của hàm số mũ trên một đoạn
Đây là dạng toán thuộc chuyên đề hàm số mũ và logarit thường xuất hiện thêm trong các thắc mắc phương trình hàm số mũ, bất phương trình hàm số mũ áp dụng - vận dụng cao của các đề thi. Để làm cho được các bài tập hàm số nón dạng này, các em cần thực hiện lần lượt theo 3 cách sau đây:
Bước 1: tính y’, tìm các nghiệm $x_1$, $x_2$,... $x_n$ trực thuộc $
Bước 2: Tính $f(a)$, $f(b)$, $f(x_1)$,... $f(x_n)$.
Bước 3: So sánh các giá trị vừa tính được sinh sống trên và kết luận GTLN, GTNN của hàm số
GTNN $m$ là số bé dại nhất trong những giá trị tính được.
GTLN M là số khủng nhất trong số giá trị tính được.
Cụ thể hơn về dạng bài bác tập hàm số mũ này, ta xét lấy ví dụ như sau:


2.2. Các dạng bài xích tập hàm số logarit thuộc chăm đề hàm số mũ cùng logarit
Dạng 1: tìm kiếm tập xác minh của hàm số logarit
Đây là dạng rất cơ bạn dạng trong bài bác tập hàm số logarit. Khi tiến hành giải, các em nhờ vào 2 phép tắc sau:
+ Hàm số $y=a^x$ nên điều kiện: alà số thực dương và a không giống 1.
+ Hàm số $y=log_ax$ buộc phải điều kiện: Số thực a dương cùng khác 1, $x>0$.
Ví dụ minh hoạ:
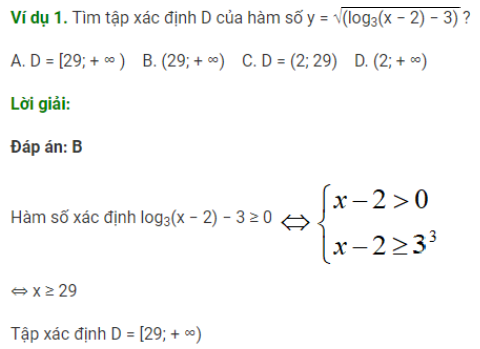
Dạng 2: Tính đạo hàm của hàm số logarit
Ở dạng này, bọn họ vận dụng những công thức đạo hàm, đạo hàm logarit để triển khai biến đổi. Họ cùng xét lấy ví dụ minh hoạ về 1 cách biến đổi tìm đạo hàm logarit sau:
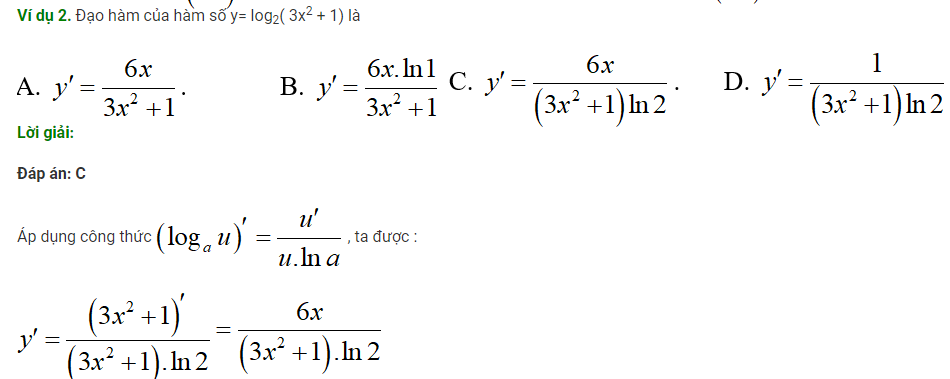
Dạng 3: Ứng dụng đạo hàm vào điều tra đồ thị hàm logarit
Đây là bước nâng cấp hơn của các bài tập dạng 2, nghĩa là sau khoản thời gian tìm đạo hàm vấn đề sẽ yêu mong thêm những em một bước nữa đấy là khảo sát và vẽ thiết bị thị hàm số vẫn cho. Ở đây, họ áp dụng những kiến thức về rất trị của hàm số, giá chỉ trị bự nhất, giá trị bé dại nhất… nhằm giải bài xích toán.
Để rõ hơn, ta thuộc xét ví dụ như minh hoạ sau đây:


Dạng 4: rất trị hàm số logarit cùng min - max nhiều biến
Đây là dạng toán ở mức độ vận dụng - vận dụng cao. Để giải được các bài tập dạng này, các em yêu cầu vận dụng xuất sắc các công thức biến đổi và gắng chắc các đặc điểm của hàm số logarit.
Cùng capnuochaiphong.com xét 2 ví dụ sau đây để hiểu cách làm dạng toán cực trị cùng min max này nhé!
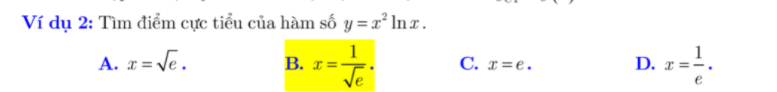
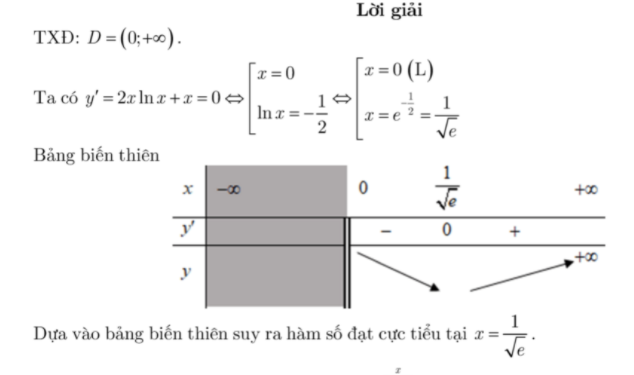
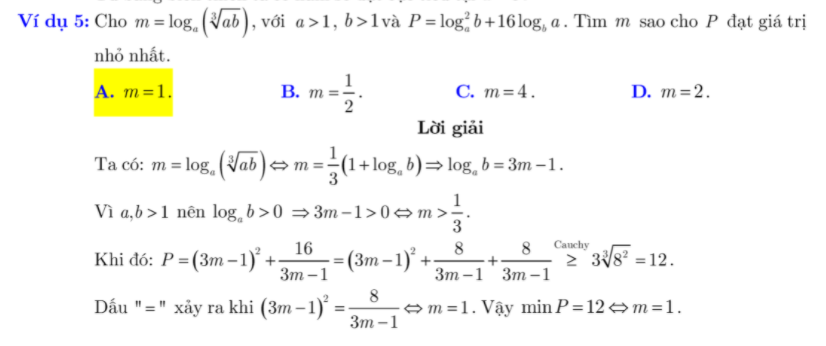
3. Bài bác tập vận dụng hàm số mũ với logarit
Để áp dụng tốt hàm mũ logarit hơn tương tự như rút ngắn thời gian suy nghĩ hay thừa nhận diện đề bài, chỉ bao gồm một phương pháp duy tuyệt nhất là các em cần luyện tập thật những để quen tay quen thuộc mắt. capnuochaiphong.com đã soạn và tổng hòa hợp riêng đến em bộ tài liệu tổng hợp bài bác tập hàm số mũ cùng logarit kèm giải cụ thể cực khá đầy đủ tất cả các dạng trong lịch trình học cũng như đề thi. Những em nhớ mua về để luyện tập hàng ngày nhé!
Tải xuống file bài xích tập hàm số mũ với logarit kèm giải chi tiết
Ngoài ra, những em hoàn toàn hoàn toàn có thể tham khảo các phương pháp giải hay, tips chọn đáp án chuẩn từ thầy Thành Đức Trung - thầy giáo Toán chăm ôn thi đại học điểm 8+ của phòng capnuochaiphong.com. Thầy đã gồm buổi livestream giải bài bác tập toán 12 hàm số mũ cùng logarit cực hữu dụng tại đoạn clip dưới đây, những em nhớ xem để học những phương pháp giải hay ho của thầy nhé!
Bài viết vẫn tổng hợp toàn cục lý thuyết hàm nón logarit và bài bác tập chi tiết về phần kỹ năng hàm số mũ cùng logarit. Chúc những em luôn đạt điểm cao và học xuất sắc nhé!















