Tính chất của đường trung tuyếcác điểm tham quan ở humua thêm dung lượng 4g viettethẻ visa dùng để làm gì
Đường trung trực của một đoạn thẳng là gì? tính chất đường trung trực được áp dụng ra làm sao trong giải toán học. Bạn đang loay hoay cùng với phần kiến thức về đường trung trực của đoạn thẳng, của tam giác cũng giống như nhiều dạng toán liên quan.
Đường trung trực của một đoạn thẳng là phần kiến thức với học viên lớp 7, khi mà lại toán hình học tập đã bắt đầu cao hơn một nấc, nhưng mà đừng vội lo lắng với toán tương quan đến mặt đường trung trực bạn chỉ việc nhớ quan niệm cùng những đặc thù hay định lý mà lại thôi. Hãy thuộc La Factoria Web chúng tôi tổng kết hầu hết nội dung đề nghị nhớ, những dạng bài xích tập cùng giải pháp giải tác dụng dễ nhớ ngay dưới đây.
Bạn đang xem: Tính chất của đường trung tuyếcác điểm tham quan ở humua thêm dung lượng 4g viettethẻ visa dùng để làm gì

Nội dung bài xích viết
Tính chất của đường trung trực Tính chất tía đường trung trực trong tam giácCác dạng toán về đường trung trực của đoạn thẳngĐịnh nghĩa con đường trung trực của đoạn thẳng là gì?
Định nghĩa: Đường thẳng trải qua trung điểm của đoạn thẳng và vuông góc cùng với đoạn thẳng gọi là con đường trung trực của đoạn thẳng ấy.
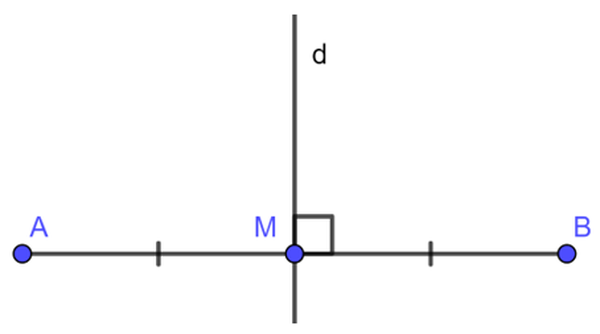
Định lý 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì giải pháp đều hai mút của đoạn thẳng đó.
GT: d là trung trực của AB, M ∈ d
=> KL: MA = MB
Định lí 2:
Điểm giải pháp đều hai đầu mút của một đoạn thẳng thì nằm trên phố trung trực của đoạn thẳng đó
Nhận xét: Tập hợp những điểm giải pháp đều hai mút của một đoạn thẳng là con đường trung trực của đoạn trực tiếp đó.
Tính chất của đường trung trực
– đặc thù đường trung trực một quãng thẳng
Mọi điểm nằm trên đường trung trực của một quãng thẳng đều phương pháp đều hai đầu mút của đoạn thẳng ấy
Trên mẫu vẽ trên, dd là con đường trung trực của đoạn trực tiếp AB. Ta cũng nói: A đối xứng với B qua d.
=> thừa nhận xét: Tập hợp những điểm giải pháp đều hai mút của một đoạn thẳng là đường trung trực của đoạn trực tiếp đó.
Tính chất cha đường trung trực trong tam giác
Với tam giác thường– ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này bí quyết đều cha đỉnh của tam giác đó.
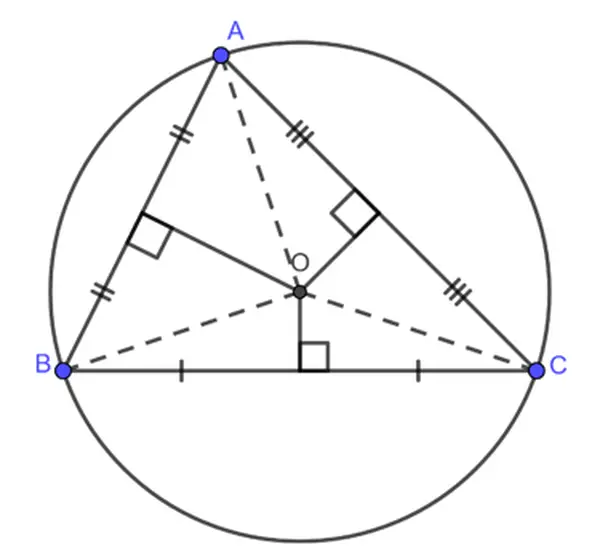
Trên hình, điểm O là giao điểm những đường trung trực của ΔABC.ΔABC.
Ta gồm OA = OB = OC. Điểm OO là tâm đường tròn nước ngoài tiếp ΔABC.ΔABC.
– Giao điểm của cha đường trung trực của một tam giác là trọng tâm đường tròn nước ngoài tiếp tam giác đó.
O là giao điểm của cha đường trung trực của tam giác ABC. Lúc đó, O là trung khu đường tròn nước ngoài tiếp tam giác ABC
Với tam giác cân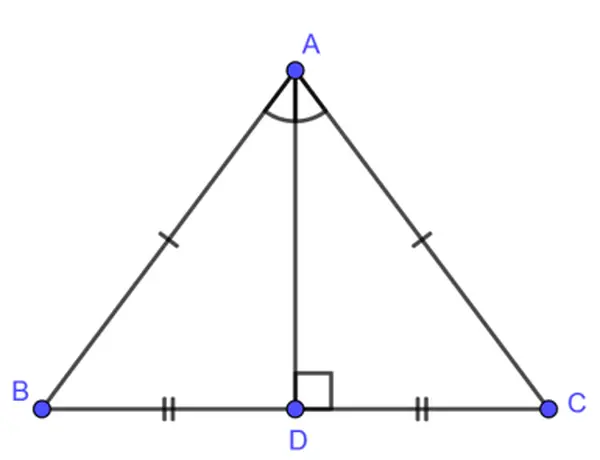
Trong tam giác cân, đường trung trực ứng với cạnh đáy đồng thời là mặt đường phân giác, đường trung con đường và đường cao cùng bắt nguồn từ đỉnh đối diện với cạnh đó.
Với tam giác vuôngTrong tam giác vuông, giao điểm của tía đường trung trực đó là trung điểm của cạnh huyền.
Các dạng toán về đường trung trực của đoạn thẳng
Dạng 1: chứng tỏ đường trung trực của một đoạn thẳng
Dạng 1: Toán chứng tỏ đường trung trực của một quãng thẳng
Phương pháp giải:
Chứng minh d là mặt đường trung trực của đoạn trực tiếp AB, ta minh chứng d cất hai điểm và phương pháp đều A cùng B hoặc sử dụng định nghĩa mặt đường trung trực.
Dạng 2: chứng tỏ hai đoạn thẳng bởi nhau
Dạng 2: minh chứng hai đoạn thẳng bằng nhau
Phương pháp:
Áp dụng định lý: “Điểm nằm trên đường trung trực của một quãng thẳng thì biện pháp đều nhị mút của đoạn trực tiếp đó.”
Dạng 3: việc về giá chỉ trị bé dại nhất
Dạng 3: việc về giá chỉ trị nhỏ nhất
Phương pháp:
Áp dụng đặc điểm đường trung trực để cầm độ lâu năm một đoạn trực tiếp thành độ nhiều năm một đoạn thẳng khác bằng nó.
Sau đó là áp dụng bất đẳng thức tam giác để tìm giá trị bé dại nhất.
Dạng 4: xác định tâm đường tròn ngoại tiếp tam giác
Dạng 4: xác định tâm con đường tròn ngoại tiếp tam giác
Phương pháp:
Áp dụng tính chất giao điểm 3 con đường trung trực của tam giác
Định lý: cha đường trung trực của một tam giác cùng đi qua một điểm. Điểm này bí quyết đều tía đỉnh của tam giác đó.
Dạng 5: bài toán về mặt đường trung trực so với tam giác cân
Dạng 5: bài bác toán liên quan đến mặt đường trung trực đối với tam giác cân
Phương pháp:
Cần ghi nhớ trong tam giác cân, đường trung trực của cạnh đáy đồng thời là đường trung tuyến , mặt đường phân giác ứng với cạnh đáy này.
Dạng 6: vấn đề về mặt đường trung trực so với tam giác vuông
Dạng 6: bài toán tương quan đến đường trung trực đối với tam giác vuông
Phương pháp:
Cần ghi nhớ với áp dụng: trong tam giác vuông, giao điểm các đường trung trực là trung điểm cạnh huyền.
Bạn rất có thể tham khảo bài học kinh nghiệm về Đường trung trực tại đây:
Một số thắc mắc về mặt đường trung trực của đoạn thẳng
Mỗi đoạn thẳng có bao nhiêu mặt đường trung trực? mỗi đoạn thẳng chỉ gồm một mặt đường trung trực, là con đường thẳng đi qua trung điểm cùng vuông góc cùng với đoạn thẳng đó.
Cách viết phương trình con đường trung trực của đoạn thẳng?
Dựa vào khái niệm và đặc thù của đường trung trực cộng với tính chất của vectơ, bao gồm 2 cách thức viết phương trình mặt đường trung trực của đoạn thẳng:
tra cứu vectơ pháp con đường của con đường trung trực và 1 điều mà nó đi qua. Áp dụng đặc thù 1 sinh hoạt trên.Bài tập áp dụng cách 1: search vectơ pháp tuyến
Cho A(1;-4) với B(3;2), viết pt tổng thể đường trung trực của đoạn AB.
Giải:
Vectơ AB = (3 – 1 ; 2 – (-4)) = (2; 6) = 2 (1; 3)
=> Vectơ pháp tuyến đường của đường trung trực của đoạn AB là : Vectơ n = (1; 3)
Gọi I(x;y ) là trung điểm của AB
x = (1 + 3 ) / 2 = 2
Và y = (- 4 + 2)/ 2 = -1
=> I(2; -1)
Phương trình tổng thể đường trung trực của đoạn AB :
a(x – x0) + b(y – y0 ) = 0
x – 2 + 3(y + 1 ) = 0
=> x + 3y + 1 = 0
Bài tập về đường trung trực của đoạn thẳng
Bài 44 (trang 76 SGK Toán 7 tập 2): hotline M là điểm nằm trên đường trung trực của đoạn trực tiếp AB, cho đoạn thẳng MA bao gồm độ nhiều năm 5cm. Hỏi độ dài MB bằng bao nhiêu?
Bài giải:
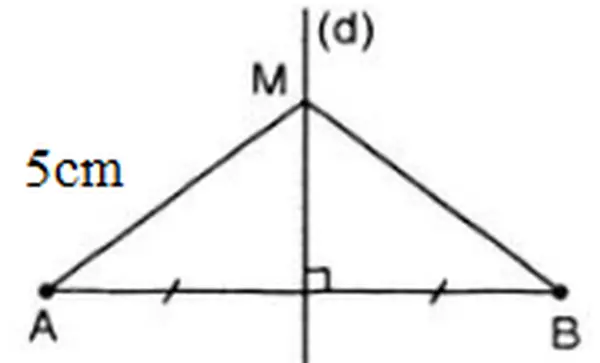
Điểm M thuộc mặt đường trung trực của AB
=> MA = MB (định lí thuận)
Vì MA = 5cm đề xuất MB = 5cm
Kiến thức áp dụng: phụ thuộc định lí về tính chất của các điểm thuộc đường trung trực (định lý thuận): Điểm nằm trê tuyến phố trung trực của một đoạn thẳng thì phương pháp đều nhị mút của đoạn thẳng đó.
Bài 45 (trang 76 SGK Toán 7 tập 2): chứng tỏ đường trực tiếp PQ được vẽ như trong hình đúng là đường trung trực của đoạn trực tiếp MN.
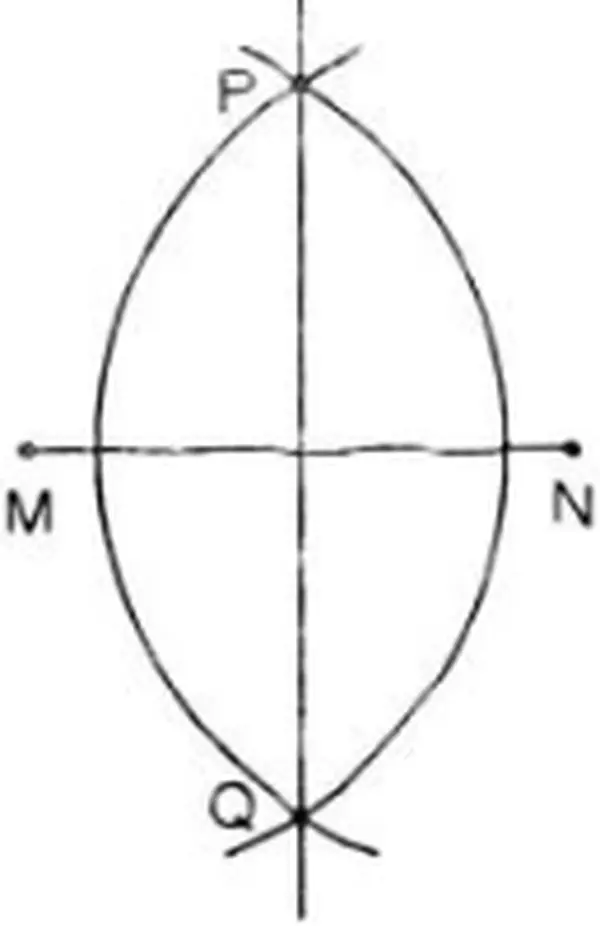
Lời giải:
Ta có: nhị cung tròn trung tâm M và N có bán kính bằng nhau và cắt nhau trên P, Q.
Nên MP = NP và MQ = NQ
=> P; Q phương pháp đều hai mút M, N của đoạn thẳng MN
nên theo định lí 2 : P; Q thuộc đường trung trực của MN
hay mặt đường thẳng qua P, Q là mặt đường trung trực của MN.
Vậy PQ là đường trung trực của MN.
Bài 46 (trang 76 SGK Toán 7 tập 2): Cho tía tam giác cân ABC, DBC, EBC tất cả chung đáy BC. Chứng tỏ ba điểm A, D, E thẳng hàng.
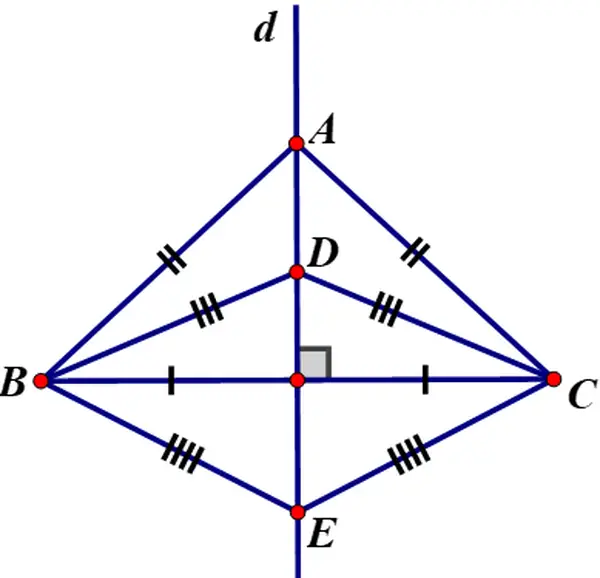
Lời giải:
Vì ΔABC cân tại A ⇒ AB = AC
=> A thuộc mặt đường trung trực của BC.
Vì ΔDBC cân nặng tại D ⇒ DB = DC
=> D thuộc con đường trung trực của BC
Vì ΔEBC cân nặng tại E ⇒ EB = EC
=> E thuộc mặt đường trung trực của BC
Do kia A, D, E thuộc thuộc con đường trung trực của BC
Vậy A, D, E trực tiếp hàng
Bài 47 (trang 76 SGK Toán 7 tập 2): mang đến hai điểm M, N nằm trê tuyến phố trung trực của đoạn thẳng AB. Chứng tỏ ΔAMN = Δ BMN.
Bài giải:
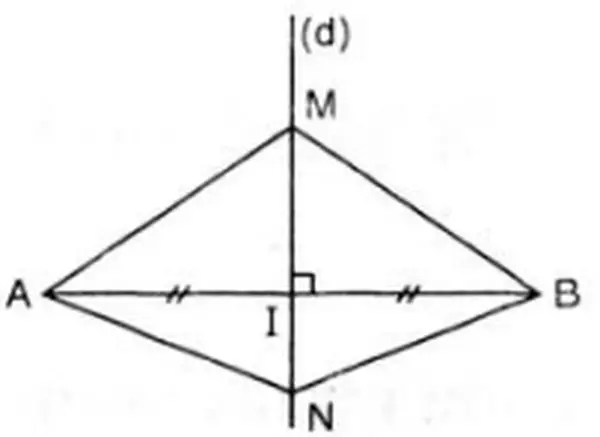
Vì M thuộc con đường trung trực của AB
=> MA = MB (định lý thuận về tính chất của những điểm thuộc đường trung trực)
N thuộc mặt đường trung trực của AB
=> na = NB (định lý thuận về tính chất của những điểm thuộc mặt đường trung trực)
Do kia ΔAMN cùng ΔBMN có:
AM = BM (cmt)
MN chung
AN = BN (cmt)
⇒ ΔAMN = ΔBMN (c.c.c)
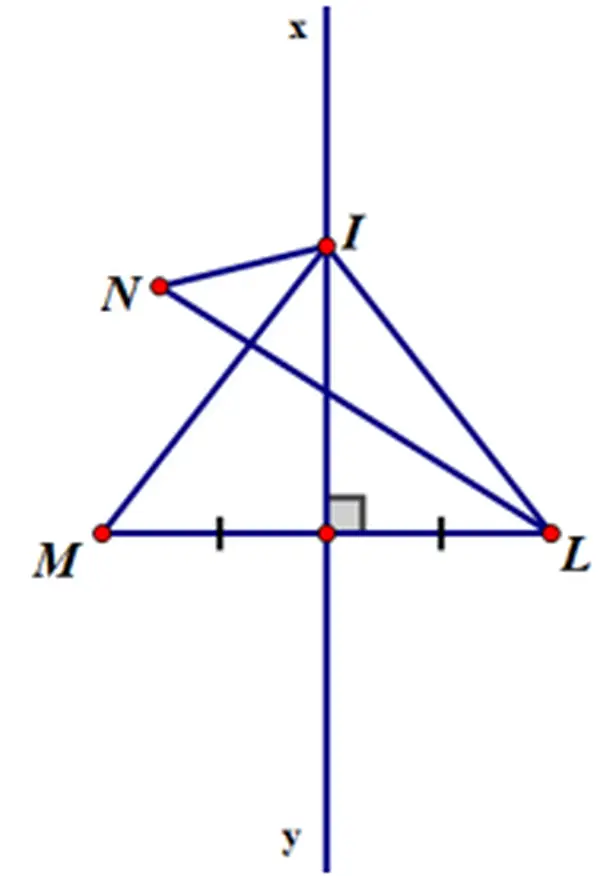
Bài 48 (trang 77 SGK Toán 7 tập 2): nhì điểm M và N thuộc nằm bên trên một nửa khía cạnh phẳng bờ là mặt đường thẳng xy. đem điểm L đối xứng với M qua xy. điện thoại tư vấn I là 1 trong điểm của xy. Hãy so sánh IM + IN cùng với LN.
Bài giải:
Vì L và M đối xứng qua con đường thẳng xy đề xuất xy là đường thẳng trải qua trung điểm với vuông góc cùng với ML.
Nên con đường thẳng xy là trung trực của ML.
I ∈ xy => lặng = IL (theo định lý 1).
Nên lặng + IN = IL + IN
– TH1: ví như I, L, N trực tiếp hàng
=> IL + IN = LN (vì N và L nằm không giống phía so với đường thẳng xy với I vị trí xy).
=> yên ổn + IN = LN
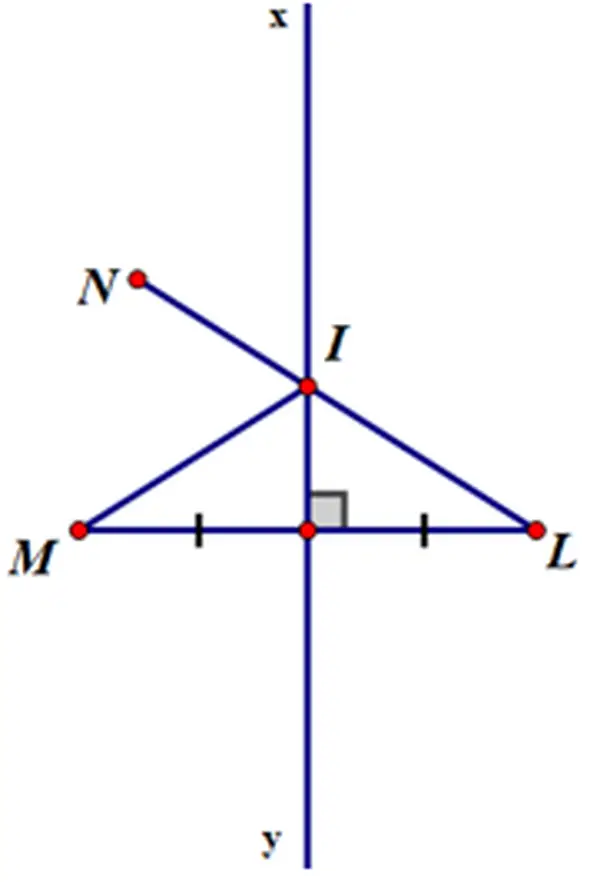
TH2: giả dụ I ko là giao điểm của LN với xy thì cha điểm I, L, N ko thẳng hàng
Áp dụng bất đẳng thức tam giác vào Δ INL ta được: IL + IN > LN
mà yên ổn = IL (cmt)
=> IL + IN > LN (bất đẳng thức tam giác)
=> yên + IN > LN
Vậy với mọi vị trí của I trên xy thì yên ổn + IN ≥ LN
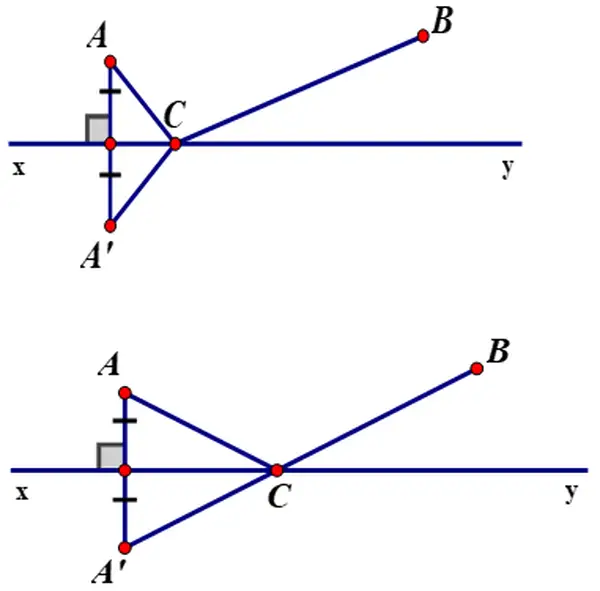
Bài 49 (trang 77 SGK Toán 7 tập 2): Hai xí nghiệp được xây dựng bên bờ một con sông tại hai vị trí A và B (h.44). Hãy tìm trên kè sông một địa điểm C để tạo ra một trạm bơm chuyển nước về đến hai đơn vị máy làm thế nào cho độ dài đường ống dẫn nước là ngắn nhất?
Lời giải:
Gọi con đường thẳng xy là bên bờ sông cần xây trạm bơm.
=> vấn đề đưa về: hai điểm A, B cố định và thắt chặt cùng nằm tại nửa khía cạnh phẳng bờ là con đường thẳng xy. Tìm địa chỉ điểm C nằm trên phố xy làm sao cho CA + CB nhỏ nhất.
Gọi A’ là điểm đối xứng của A qua mặt đường thẳng xy.
Theo như chứng tỏ ở bài 48 ta có: CA + CB = CA’ + CB ≥ A’B (A’B nỗ lực định).
=> CA + CB đạt ngắn nhất bởi A’B.
Dấu “=” xảy ra khi CA’+CB = A’B, tức là A’; B; C thẳng hàng giỏi C là giao điểm của A’B và xy.
Vậy vị trí đặt trạm bơm là giao điểm của đường thẳng xy với đường thẳng A’B, trong số đó A’ là vấn đề đối xứng với A qua xy
Bài 51 (trang 77 SGK Toán 7 tập 2): cho đường thẳng d với điểm phường không vị trí d. Hình 46 minh họa cho phương pháp dựng con đường thẳng đi qua điểm phường vuông góc với con đường thẳng d bằng thước với compa như sau:
(1) Vẽ con đường tròn tâm p với bán kính thích hợp làm thế nào cho nó bao gồm cắt d tại nhị điểm A và B.
(2) Vẽ hai tuyến phố tròn với bán kính bằng nhau bao gồm tâm tại A và B làm sao cho chúng cắt nhau. Gọi một giao điểm của bọn chúng là C (C ≠ P)
(3) Vẽ con đường thẳng PC.
Em hãy chứng tỏ đường thẳng PC vuông góc với d.
Bài giải:
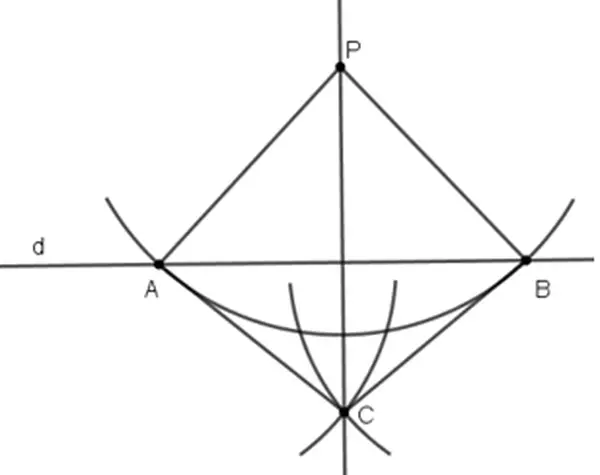
CA = CB (C nằm trong 2 cung tròn trung ương A, B nửa đường kính bằng nhau) buộc phải C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
b) Một cách vẽ khác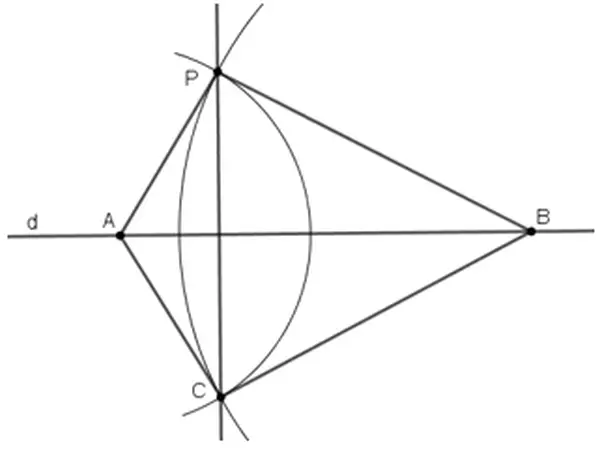
– mang hai điểm A, B bất kỳ trên d.
– Vẽ cung tròn chổ chính giữa A bán kính AP, cung tròn trung khu B bán kính BP. Nhị cung tròn giảm nhau tại C (C khác P).
– Vẽ đường thẳng PC. Lúc đó PC là đường đi qua p và vuông góc với d
Chứng minh :
– Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn chổ chính giữa A nửa đường kính PA)
=> A thuộc con đường trung trực của PC.
PB = CB (P, C thuộc thuộc cung tròn tâm B bán kính PB)
=> B thuộc con đường trung trực của PC.
=> AB là đường trung trực của PC
=> PC ⏊ AB giỏi PC ⏊ d.
Hy vọng với phần kiến thức và kỹ năng cần nhớ cũng giống như các dạng toán thân thuộc về con đường trung trực đã share ở trên các bạn sẽ dễ dàng hơn trong việc giải các bài tập liên quan. Định lí và có mang về đường trung trực là nhì phần đặc biệt nhất buộc chúng ta phải ở trong lòng nhằm áp dụng sớm nhất vào giải toán. Hình học luôn có sự thú vui khi càng lên bậc cao hơn, mặt đường trung trực chính là bài học tập nền tảng cho bạn sau này.















